First Shader

In this step, you will create your first shader using the WGSL language. You will learn how to define entry points, shader attributes, and how to write a simple shader vertex and a fragment shader that outputs a solid color in a triangle.

The vertex shader is responsible for transforming the vertices of a 3D object into screen space. In this step, we will create a simple vertex shader that passes the vertex position to the fragment shader.

@vertex
fn vtx_main(@builtin(vertex_index) vertex_index : u32)
-> @builtin(position) vec4f {
  const pos = array(
    vec2( 0.0,  0.5),
    vec2(-0.5, -0.5),
    vec2( 0.5, -0.5)
  );
  return vec4f(pos[vertex_index], 0, 1);
}

In the vertex shader above, we define the vtx_main function as the entry point for the vertex shader. The @vertex decorator indicates that this function is a vertex shader. The @builtin(vertex_index) attribute specifies the input parameter vertex_index as the index of the vertex being processed.

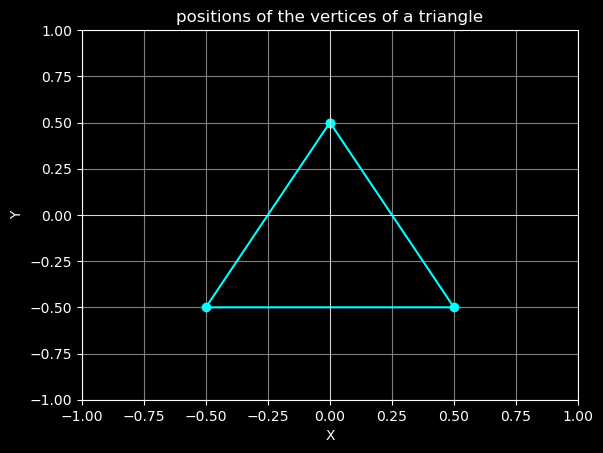
The pos constant is a matrix representing the positions of the vertices of a triangle. The vertex_index parameter is used to index into this array to get the position of the current vertex.

The function returns a 4D vector vec4f representing the position of the vertex in homogeneous ¹ coordinates. The vec4f constructor takes the 2D position of the vertex from the pos array and sets the z and w components to 0 and 1, respectively.

The @builtin(position) attribute specifies that the return value of the function is the position of the vertex in clip space.

@fragment
fn frag_main() -> @location(0) vec4f {
  return vec4(1, 1, 1, 1);
}

In the fragment shader above, we define the frag_main function as the entry point for the fragment shader. The @fragment decorator indicates that this function is a fragment shader.

The function returns a 4D vector vec4f representing the color of the fragment. The vec4 constructor takes the RGBA color values as input. In this case, we return white color (1, 1, 1, 1).

You can now run the shader and see the output in your browser using the editor page.

References: